TRAZO DE LÍNEAS RECTAS
Las líneas en OpenGL son en realidad segmentos acotados, en lugar de la idea matemática de rectas infinitas. Su definición viene dada por la especificación del valor de sus dos vértices extremos.
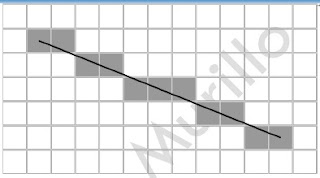
Consideremos una línea recta que pasa por dos puntos P1=[20, 20] y [25,20]. Podemos calcular la línea recta que pasa por estos puntos como
(y-y1) = (y2-y1)*(x-x1)/(x2-x1)
Sustituyendo los valores tenemos
(y-20) = (21-20)*(x-20)/(25-20)
Finalmente tenemos
y = 0.2 x + 16
Podemos calcular los valores utilizando el siguiente código
void linea(int x0, int y0, int x1, int y1)
{ int x;
float dy, dx, y, m;
dy = y1 - y0;
dx = x1 - x0;
m = dy/dx;
y = y0;
for(x = x0; x <= x1; x++)
{ escribir_pixel(x, (int) floor(y+0.5) );
y +=m; } }
Note que se suma 0.5 y se calcula la parte entera para redondear la solución.
REPRESENTACION Y TRAZO DE POLIGONOS
OpenGL maneja polígonos correctamente siempre y cuando sean simples y convexos. Si ese no es el caso, OpenGL dibuja cosas raras.
Además en algunas ocasiones se quiere especificar el vector normal del plano en el cual se encuentra el polígono. Dicho vector normal se necesita p.e. para algoritmos de visualización avanzada (``Phong shading'').
Cuando se escriben aplicaciones gráficas nos enfrentamos con el problema siguiente: desde alguna fuente ``vienen'' listas de puntos (o bien de otro programa, o bien de un fichero, o bien de modo interactivo) y hay que interpretar las listas como polígonos, es decir, hay que verificar si las listas cumplen la definición de especificar polígonos simples y convexos. Si ese no es el caso, a lo mejor se pueden ``corregir'' las listas. (Programas con tal propiedades se llama robustos y tolerantes.)
Entonces (en el caso de mera visualización con OpenGL):
Se puede eliminar puntos múltiples consecutivos en la lista.
Se puede intentar calcular el plano en el cual se encuentran más o menos los puntos del polígono (eso no es tan trivial).
En dicho plano, es decir, una vez corregidos los puntos hasta que se encuentren exactamente en el plano, se puede verificar si el polígono es simple y convexo (eso es algo bastante fácil).
Si no es así, se podría subdividir el polígono en partes simples y convexos para seguir trabajando después con las partes sin problemas (este paso no lo vamos a realizar en estas prácticas).
Antes de dedicarnos a los detalles, dibujamos polígonos con OpenGL asumiendo que la lista de puntos cumple la definición.
Siempre que se quiera dibujar un objeto de OpenGL (en este caso unos polígonos, antes vimos puntos y segmentos), hay que decírselo de antemano con la función
glBegin()
La lista de puntos se define con consecutivas llamadas a
glVertex*()
y se termina el trabajo con
glEnd()
En lugar de dibujar polígonos rellenados, OpenGL puede dibujar, o bien solo las esquinas o bien solo los segmentos del borde. Eso se realiza con la función
glPolygonMode()
a la cual hay que pasar también cuál de las dos posibles caras del polígono se quiere pintar.
Además se pueden llenar los polígonos con patrones que no detallamos por el momento.
glEnable()
glPolygonStipple()
ALGORITMO DDA PARA GENERACIÓN DE LÍNEAS
El algoritmo de Bresenham es un algoritmo creado para dibujar rectas en los dispositivos de gráficos rasterizados, como por ejemplo un monitor de ordenador, que determina qué pixeles se rellenarán, en función de la inclinación del ángulo de la recta a dibujar.
Este Algoritmo sirve para Generar Una Línea Recta , y Para eso Hace Uso de La pendiente Y de los Incrementos en X, Y
El Código es el Siguiente:
void DDA(int x_0,int y_0, int x_fin, int y_fin){
glClear ( GL_COLOR_BUFFER_BIT );
glPointSize(3.0);
glScalef(4.0, 4.0, 2.0);
glPointSize(3.0);
glScalef(4.0, 4.0, 2.0);
glBegin(GL_POINTS);
glVertex2i(x_0,y_0);
glVertex2i(x_0,y_0);
int vx=(int)fabs(x_fin-x_0);
int vy=(int)fabs(y_fin-y_0);
int dx,dy;
int m = (int)(y_fin-y_0)/(x_fin-x_0);
int vy=(int)fabs(y_fin-y_0);
int dx,dy;
int m = (int)(y_fin-y_0)/(x_fin-x_0);
if(m==1)m++;
if(m==0)m=-1;
if(m==0)m=-1;
if(m>0&&m<1){
if(x_0<x_fin){
dx=1;
dy=m;
}else{
dx=-1;
dy=-m;
}
}
else
if(m>0&&m>1){
if(m>1){
if(x_0<x_fin){
dy=1;
dx=(int)1/m;
if(x_0<x_fin){
dx=1;
dy=m;
}else{
dx=-1;
dy=-m;
}
}
else
if(m>0&&m>1){
if(m>1){
if(x_0<x_fin){
dy=1;
dx=(int)1/m;
}else{
dy=-1;
dx=(int)-1/m;
dy=-1;
dx=(int)-1/m;
}
}else
if(m<0&&fabs(m)<1){
if(x_0>x_fin)
{
dx=-1;
dy=-m;
{
dx=-1;
dy=-m;
}else
{
dx=1;
dy=-m;
}
{
dx=1;
dy=-m;
}
}
else{
if(x_0>x_fin){
dy=1;
dx=-1/m;
dy=1;
dx=-1/m;
}
else {
dy=-1;
dx=1/m;
else {
dy=-1;
dx=1/m;
}
}
if(m>0&&m<1){
for(int i=1;i<=vx;i++)
{
glVertex2i(x_0+dx ,y_0+dy );
x_0+=dx;
y_0+=dy;
for(int i=1;i<=vx;i++)
{
glVertex2i(x_0+dx ,y_0+dy );
x_0+=dx;
y_0+=dy;
}
}
else
if(m>0&&m>1){
for(int i=1;i<=vy;i++){
glVertex2i(x_0+dx ,y_0+dy );
x_0+=dx;
y_0+=dy;}
}
else
if(m>0&&m>1){
for(int i=1;i<=vy;i++){
glVertex2i(x_0+dx ,y_0+dy );
x_0+=dx;
y_0+=dy;}
}else
if(m<0&&fabs(m)<1){
for(int i=1;i<=vx;i++)
{
glVertex2i(x_0+dx ,y_0+dy );
x_0+=dx;
y_0+=dy;
{
glVertex2i(x_0+dx ,y_0+dy );
x_0+=dx;
y_0+=dy;
}
}
else{
for(int i=1;i<=vy;i++){
glVertex2i(x_0+dx ,y_0+dy );
x_0+=dx;
y_0+=dy;
}
}
}
glEnd();
glFlush();
}
glVertex2i(x_0+dx ,y_0+dy );
x_0+=dx;
y_0+=dy;
}
}
}
glEnd();
glFlush();
}
ALGORITMO DE BRESENHAM PARA TRAZAR LÍNEAS
El algoritmo de Bresenham es un algoritmo que determina los puntos en un mapa de bits de n dimensiones que deben ser trazados con el fin de formar una aproximación a una línea recta entre dos puntos dados.
Es comúnmente usado para dibujar líneas en una pantalla de ordenador, ya que utiliza sólo adición de enteros, la resta y desplazamiento de bits, que son operaciones muy barato en las arquitecturas de ordenador estándar. Es uno de los primeros algoritmos desarrollados en el campo de gráficos por ordenador. Una extensión menor a la del algoritmo original también se ocupa de dibujar círculos.
ALGORITMO DE BRESENHAM PARA TRAZAR CIRCUNFERENCIAS
En graficación, el algoritmo de “mid point circle” es un algoritmo utilizado para determinar los puntos necesarios para dibujar un círculo.
El algoritmo es una variante del algoritmo de la línea Bresenham, por lo que es a veces conocido como algoritmo de círculo Bresenham, aunque en realidad no inventada por Bresenham. El algoritmo comienza en consecuencia con el círculo de la ecuación
x2+y 2=r2.
Así, el centro del círculo se encuentra en (0,0). Consideramos que sólo la primera el octante primera y trazar una curva que comienza en el punto (r,0) y hacia arriba los ingresos ya la izquierda, llegando al ángulo de 45 °. La dirección “rápida” aquí es la dirección vertical. El algoritmo hace siempre un paso en la dirección positiva (hacia arriba), y de vez en cuando también tiene que hacer un paso en la "lenta" la dirección, la dirección x negativa. De la ecuación de un círculo se obtiene la ecuación transformada
x2+y 2-r2= 0, donde r2 se calcula sólo una sola vez durante la inicialización

No hay comentarios:
Publicar un comentario